通过BFS/DFS解决岛屿最大面积问题

Zielorem
  2023-01-13 14:57:50 2023-01-13 14:57:50 Created   2023-07-14 01:07:16 2023-07-14 01:07:16 Updated      1.5k Words  7 Mins  

Question

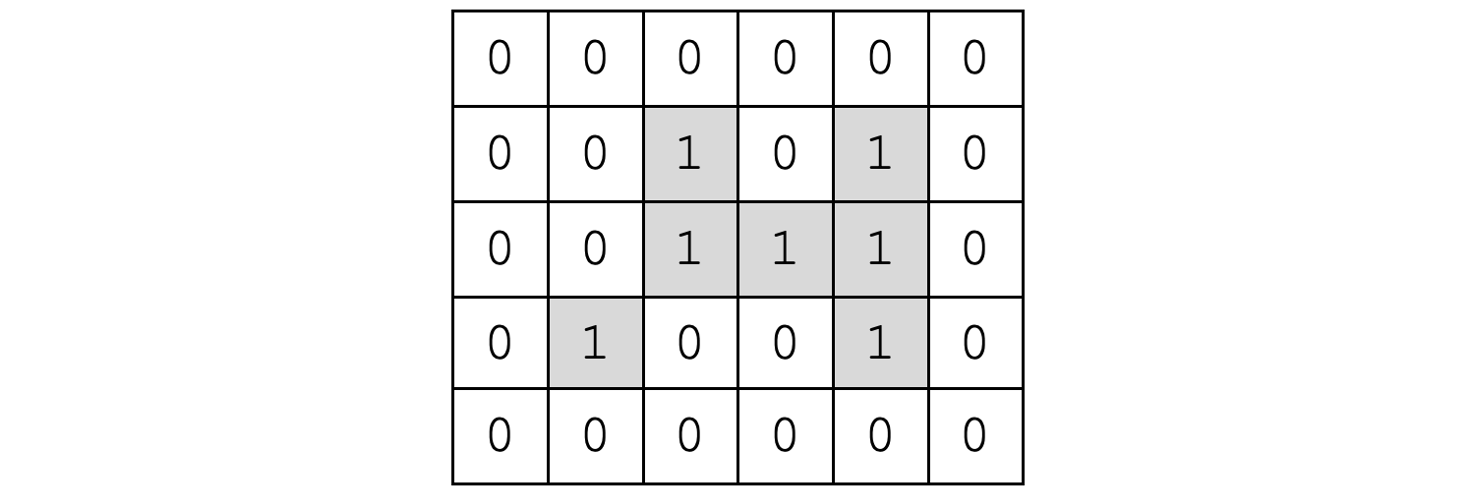
default

当前存在一个大小为m*n的二进制矩阵grid，假设岛屿是由一些相邻的1构成的组合，即两个1必须在水平或垂直的四个方向上相邻（假设grid外的位置全为0），岛屿的面积即岛上值为1的单元格的数目。计算并返回grid中最大的岛屿面积。若不存在岛屿，则返回面积为0。

steps

由于每个岛屿均被水包围，因此在登陆岛屿后，对岛上的每一寸土地进行递归即可计算当前岛屿面积，最后返回所有岛屿中所得的最大面积即可。登陆岛屿后的具体步骤为

  • 以此时所处位置为中心，向上、下、左、右四个方向前进

  • 若发现在该方向前进后抵达的新地点为水或为已抵达过的地点，则停止以该方向前进

  • 若发现在该方向前进后抵达的新地点为未抵达过的地点，则在对其进行标记后，重复步骤1

此即深度优先搜索方法，该方法实际上将所抵达的点均压至栈中，当新入栈的点抵达边界条件时，该点会在执行完毕后出栈，直至栈被清空。而将执行操作的数据结构从栈替换为队列后，算法会转变为广度优先搜索方法，即每次执行操作时均从队首取出所储存的点，并将接下来需要遍历的点置于队尾，直至队列被清空。

DFS

在以grid中每一寸土地为中心进行递归前，需要确定边界终止条件，即遍历位置抵达grid的四个边缘外的时刻。其代码为

1
2
3
4
5
6
7
int i, j;
if(i == grid.size() || i < 0){
  return 0;
}
else if(j == grid[0].size() || j < 0){
  return 0;
}

当所抵达的点为陆地时，需要将其标记为已抵达过的点，从而避免后续递归点再次对其进行遍历。因此，可将遍历后的点直接设置为0，此即著名的沉岛策略。尔后在对上、下、左、右四个方向上的地点进行递归，并同时统计该岛屿面积。加入边界终止条件后，其代码为

1
2
3
4
5
6
7
8
9
10
11
12
13
int getProportion(vector<vector<int>>& grid, int i, int j){
  if(i == grid.size() || i < 0){
    return 0;
  }
  else if (j == grid[0].size() || j < 0){
    return 0;
  }
  if(grid[i][j] == 1){
    grid[i][j] == 0
      return 1 + getProportion(grid, i + 1, j) + getProportion(grid, i - 1, j) + getProportion(grid, i, j + 1) + getProportion(grid, i, j - 1);
  }
  return 0;
}

尔后，通过主函数遍历grid中的每一个点，确定每个岛屿的面积大小，并实时更新最大岛屿面积，完整代码为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution{
  int getProportion(vector<vector<int>>& grid, int i, int j){
  if(i == grid.size() || i < 0){
    return 0;
  }
  else if (j == grid[0].size() || j < 0){
    return 0;
  }
  if(grid[i][j] == 1){
    grid[i][j] == 0
      return 1 + getProportion(grid, i + 1, j) + getProportion(grid, i - 1, j) + getProportion(grid, i, j + 1) + getProportion(grid, i, j - 1);
  }
  return 0;
}

public:
  int maxProportionOfIsland(vector<vector<int>>& grid){
    int maxProportion = 0;
    int proportion = 0;
    for(int i = 0;i < grid.size();i++){
      for(int j = 0;j < grid[0].size();j++){
        if(grid[i][j] == 1){
          proportion = getProportion(grid, i, j);
          maxProportion = maxProportion < proportion ? proportion : maxProportion;
        }
      }
    }
    return maxProportion;
  }
};

Python下代码为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
  def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
    maxArea = 0
    
    def getArea(x, y):
      if not (0 <= x < len(grid) and 0 <= y < len(grid[0])):
        return 0
      if grid[x][y] == 1:
        grid[x][y] == 0
        return 1 + getArea(x - 1, y) + getArea(x + 1, y) + getArea(x, y + 1) + getArea(x, y - 1)
      return 0
    
    for m in range(len(grid)):
      for n in range(len(grid[0])):
        if grid[m][n] == 1:
          maxArea = max(getArea(m, n), maxArea)
    return maxArea

BFS

首先建立队列，并设置操作执行过程中的终止条件。与DFS算法相同，该方法依旧采用沉岛策略，并根据队列顺序依次遍历岛屿中的点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void getArea(vector<vector<int>>& grid, int i, int j){
  queue<pair<int, int>> q;
  q.push({i, j});
  while(!q.empty()){
    auto t = q.front();
    q.pop();
    int i = t.first, j = t.second, area = 0;
    if(i < 0 || j < 0 || i == grid.size() || j == grid[0].size()){
      continue;
    }
    else if(grid[i][j] == 0){
      continue;
    }
    grid[i][j] == 0;
    area++;
    if (i > 0 && grid[i - 1][j] == 1){
      q.push({i - 1, j});
    }
    if (j > 0 && grid[i][j - 1] == 1){
      q.push({i, j - 1});
    }
    if(i <= grid.size() && grid[i + 1][j] == 1){
      q.push({i + 1, j});
    }
    if(j <= grid[0].size() && grid[i][j + 1] == 1){
      q.push({i, j + 1});
    }
  }
}

尔后，建立主函数遍历grid中的每个点，其完整代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution{
public:
  int area = 0;
  int maxAreaOfIsland(vector<vector<int>>& grid){
    int maxArea = 0;
    for(int i = 0;i < grid.size();i++){
      for(int j = 0;j < grid[0].size();j++){
        if(grid[i][j] == 1){
          area = 0;
          getArea(grid, i, j);
          maxArea = max(area, maxArea);
        }
      }
    }
    return maxArea;
  }
  void getArea(vector<vector<int>>& grid, int i, int j){
    queue<pair<int, int>> q;
    q.push({i, j});
    while(!q.empty()){
      auto t = q.front();
      q.pop();
      int i = t.first, j = t.second;
      if(i < 0 || j < 0 || i == grid.size() || j == grid[0].size()){
        continue;
      }
      else if(grid[i][j] == 0){
        continue;
      }
      grid[i][j] == 0;
      area++;
      if (i > 0 && grid[i - 1][j] == 1){
        q.push({i - 1, j});
      }
      if (j > 0 && grid[i][j - 1] == 1){
        q.push({i, j - 1});
      }
      if(i <= grid.size() && grid[i + 1][j] == 1){
        q.push({i + 1, j});
      }
      if(j <= grid[0].size() && grid[i][j + 1] == 1){
        q.push({i, j + 1});
      }
    }
  }
};

Python下代码为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
  def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
    def getArea(grid, x, y):
      queue = [[x, y]]
      while queue:
        [x, y] = queue.pop(0)
        if 0 <= x < len(grid) and 0 <= y < len(grid[0]) and grid[x][y]:
          grid[x][y] == 0
          self.area += 1
          queue += [[x - 1, y], [x + 1, y], [x, y + 1], [x, y - 1]]
      return self.area
    maxArea = 0
    for i in range(len(grid)):
      for j in range(len(grid[0])):
        if(grid[i][j] == 1):
          self.area = 0
          maxArea = max(getArea(grid, i, j), maxArea)
    return maxArea
  • Title: 通过BFS/DFS解决岛屿最大面积问题
  • Author: Zielorem
  • Created at : 2023-01-13 14:57:50
  • Updated at : 2023-07-14 01:07:16
  • Link: https://zielorem.github.io/2023/01/13/island-proportion/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
通过BFS/DFS解决岛屿最大面积问题
  1. DFS
  2. BFS