通过排列组合问题理解回溯算法

排列

Question

给定一个不含重复数字的数组nums，返回其所有可能的元素不重复的全排列。

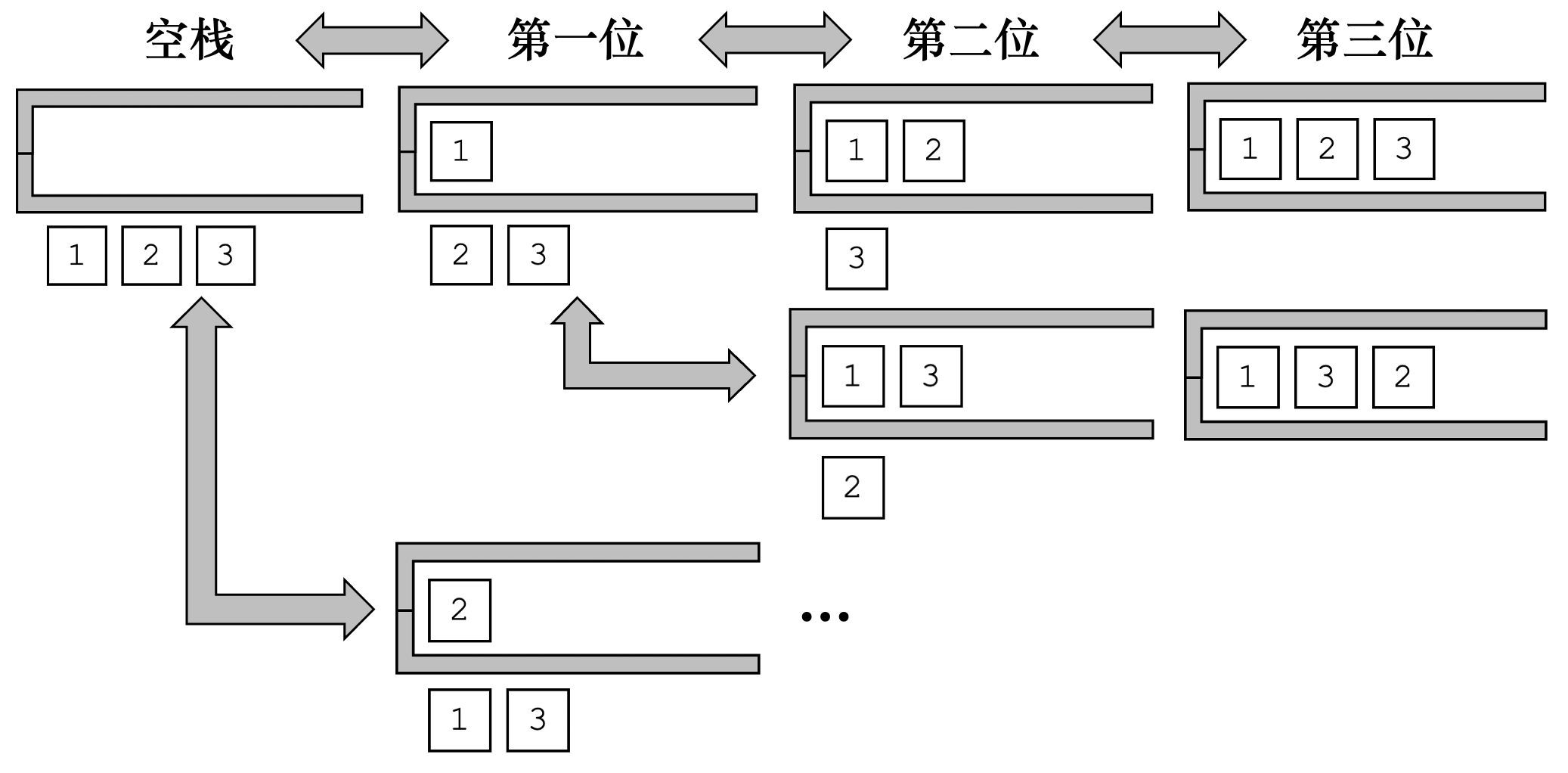
以数组[1, 2, 3]为例，其总共可能含有的全排列数为 个。一般情况下，我们会逐个选择排列中的元素以组成新排列。例如：

• 首先选择1作为排列的第一位，则第二位可以选择的元素有2和3

• 选择2作为排列的第二位，则第三位可以选择的元素仅有3

• 选择3作为排列的第三位，则该排列为[1, 2, 3]

第三步完成后，由于排列已经形成，此时需要考虑其他可能存在的排列

• 重新考虑此时排列的第三位，但3已被选过，且无其他选择，回退到上一位

• 重新考虑此时排列的第二位，由于2已被选过，因此可以选择3作为新排列的第二位

• 最后选择2作为新排列的第三位，则该排列为[1,3,2]

继续考虑其他可能存在的排列

• 重新考虑此时排列的第三位，但2已被选过，且无其他选择，回退到上一位

• 重新考虑此时排列的第二位，由于2与3均已被选过，且无其他选择，回退到上一位

• 重新考虑此时排列的第一位，由于1已被选过，可以选择的元素还有2与3

• 选择2作为新排列的第一位…

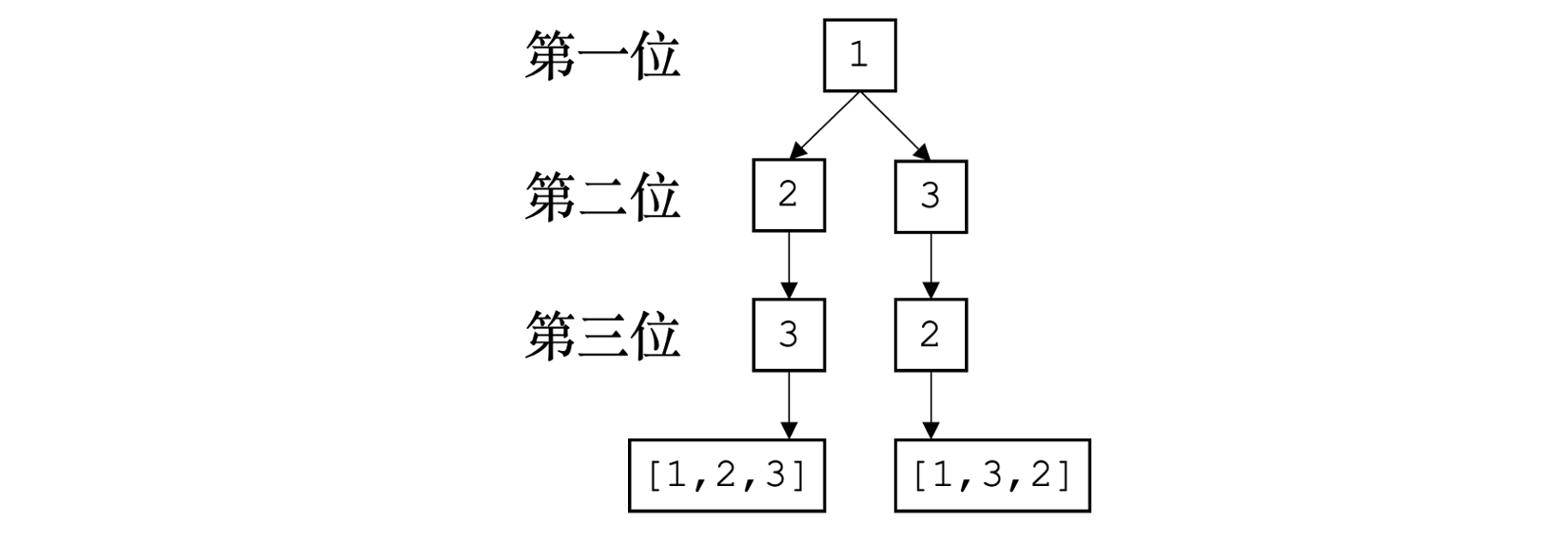
依此规律，我们可以生成所有可能存在的6个排列。将这些排列生成过程以树的形式表示后不难发现，其规律类似于之前提到的DFS算法，因此该问题可以借助DFS算法实现。另外，所谓的“重新考虑”实际上是将排列复原至前一个状态上，尔后重新选择新元素，这种类似“时光倒流”的倒退算法即为著名的回溯算法。借助回溯算法，可以解决存在多个步骤且每个步骤有多种实现方法的问题（例如本文的排列与组合问题）。

首先确定用于生成排列的容器、变量与函数

//用于生成排列的主要容器
vector<vector<int>> permute(vector<int>& nums){
  vector<vector<int>> ans;  //用于存储所有全排列结果的容器
  vector<int> path;  //用于存储全排列生成步骤（或路径）的容器（即问题分析中所使用的栈）
  vector<int> visited(n, 0);  //用于存储元素选择状况的容器
  int n = nums.size();  //即单个全排列的长度
  dfs(ans, path, nums, visited, n);  //DFS算法
  return ans;  //主函数最终返回所有全排列结果
}

尔后定义DFS算法的具体内容

void dfs(vector<vector<int>>& ans, vector<int>& path, vector<int>& nums, vector<int>& visited, int n){
  //（确定终止条件）当步骤执行至某全排列的长度等于原数组长度时，该排列生成完毕
  if(path.size() == n){
    ans.push_back(path);  //将该全排列推入结果容器中
    return;  //并返回
  }
  //用于选择元素的for循环，依次逐个选择元素直至选择完毕
  //在nums包含的n个元素中进行选择
  for(int i = 0;i < n;i++){
    //若某个元素未被选择
    if(visited[i] == 0){
      visited[i] = 1;  //则将其选择，并将其状态设置为已选择
      path.push_back(nums[i]);  //将被选择的元素推入步骤容器中（前进）
      dfs(ans, path, nums, visited, n);  //并对其执行DFS操作（继续选择该排列的下一位）
      path.pop_back();  //该排列生成完毕后将该元素推出容器（回溯）
      visited[i] = 0;  //并设置为未选择（便于之后重新选择）
    }
  }
}

其整体运行过程与前文分析部分所展示的过程一致，完整代码为

class Solution{
public:
  void dfs(vector<vector<int>>& ans, vector<int>& path, vector<int>& nums, vector<int>& visited, int n){
    if(path.size() == n){
      ans.push_back(path);
      return;
    }
    for(int i = 0;i < n;i++){
      if(visited[i] == 0){
        visited[i] = 1;
        path.push_back(nums[i]);
        dfs(ans, path, nums, visited, n);
        path.pop_back();
        visited[i] = 0;
      }
    }
  }
  vector<vector<int>> permute(vector<int>& nums){
    vector<vector<int>> ans;
    vector<int> path;
    vector<int> visited(n, 0);
    int n = nums.size();
    dfs(ans, path, nums, visited, n);
    return ans;
  }
};

组合

Question

给定两个整数n和k，返回范围 中所有可能的k个数的组合。

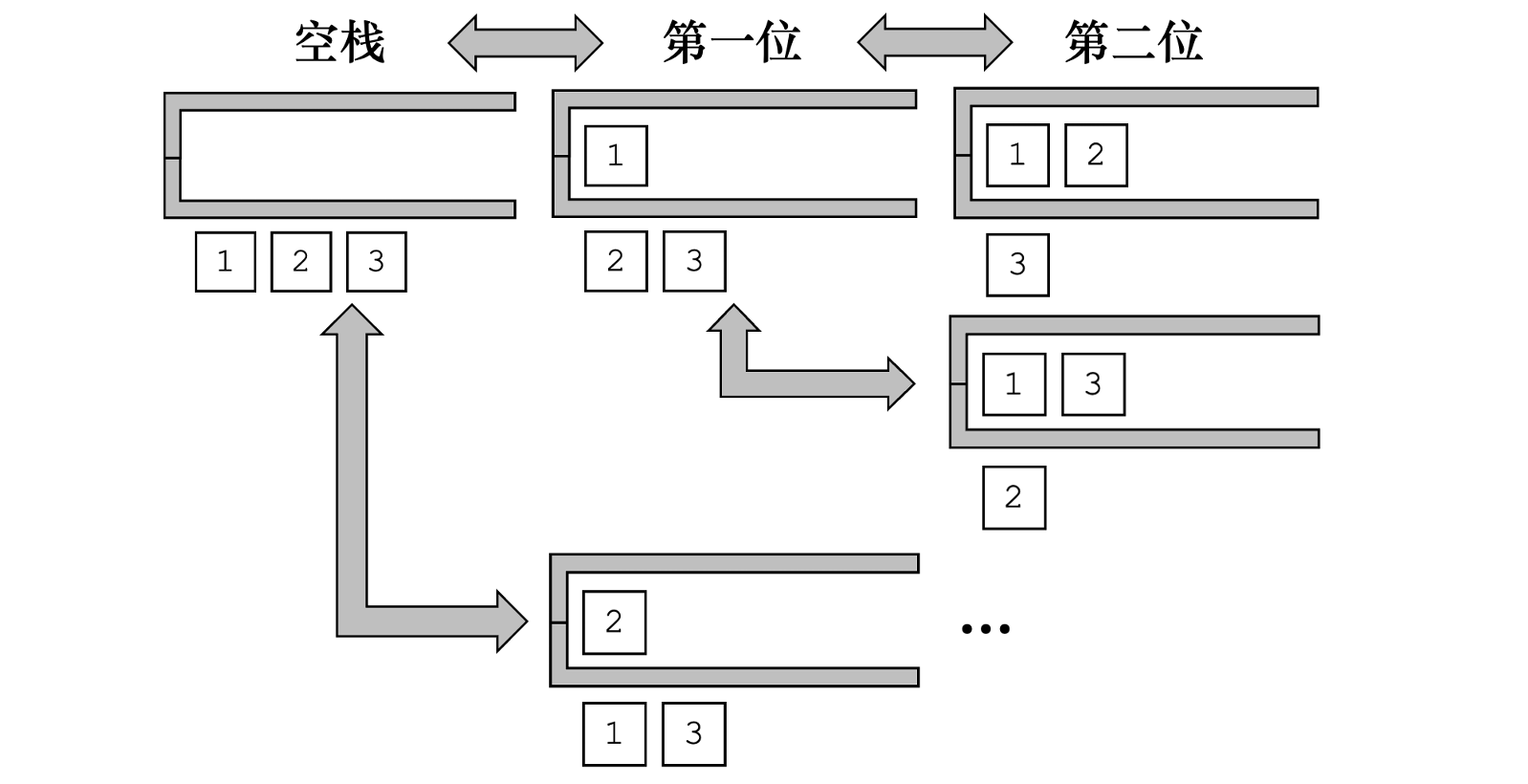
以数组[1,2,3]为例，此时若k值为2，则其总共可能含有的组合数为 个。组合问题与排列问题的区别在于前者不关注于组合内元素的排列顺序，更侧重于分析组合中存在哪些元素。因此，生成组合的过程大致为：

• 选择1作为组合的第一位，下一个可选元素有2和3

• 选择2作为组合的第二位，则该组合为[1, 2]

第二步完成后，由于组合已经形成，此时需要考虑其他可能存在的组合

• 回退至上一位

• 重新选择3作为组合的第二位，则该组合为[1, 3]

继续考虑其他可能存在的组合

• 回退至上一位，发现都已被选过，继续回退

• 重新选择2作为组合的第一位…

依此规律，我们可以生成所有可能存在的6种数组结果，其中包含了3种组合。由此可见，虽然其大致过程与处理排列问题时的流程一致，但在生成过程中难免会产生重复的组合。该生成过程在树结构下可表示为

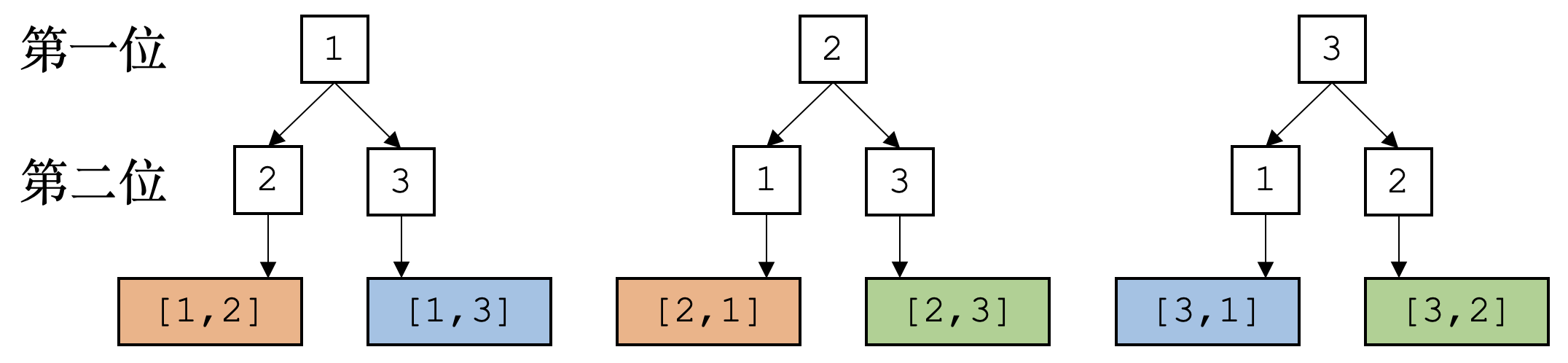
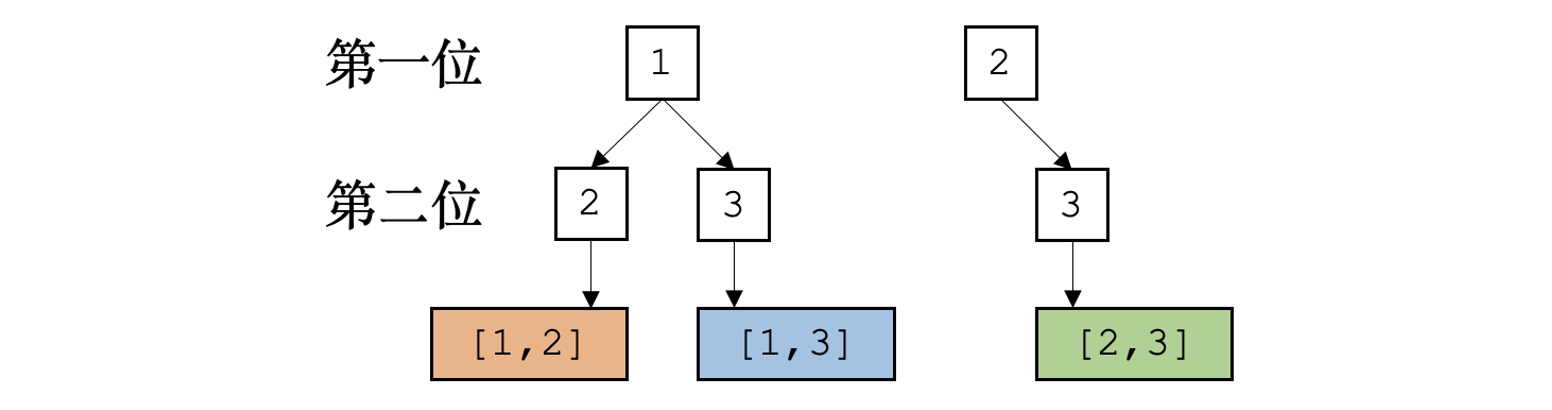
因此，我们需要去除生成结果中的重复组合，即去除上图中冗余组合所属的“枝条”，该过程一般被称为剪枝操作。通过剪枝操作，可以保证所生成的组合均不重复。经过剪枝操作后，生成过程被简化为

首先确定用于生成组合的容器、变量与函数

//用于生成组合的主要容器
vector<vector<int>> combine(int n, int k){
  vector<vector<int>> ans;  //用于存储所有组合结果的容器
  vector<int> path;  //用于存储组合生成步骤（或路径）的容器（即问题分析中所使用的栈）
  dfs(n, k, start);  //DFS算法
  return ans;  //主函数最终返回所有组合结果
}

尔后定义DFS算法的具体内容

void dfs(int n, int k, int start){
  //（确定终止条件）当步骤执行至某组合的长度等于k时，该组合生成完毕
  if(path.size() == k){
    ans.push_back(path); //将该组合推入结果容器中
    return;  //并返回
  }
  //用于选择元素的for循环，依次逐个选择元素直至选择完毕
  //从start开始循环实际上为剪枝操作，通过大小关系保证了结果的不重复性
  for(int i = start;i <= n;i ++){
    path.push_back(i);  //选择元素推入容器（前进）
    dfs(n, k, i + 1);  //执行DFS操作（选择下一位）
    path.pop_back();  //将元素推出容器（回溯）
  }
}

在该算法中，剪枝操作实际上通过for循环实现，它可以保证后续位的元素一定大于相邻的前一个元素。从组合的生成结果[[1, 2], [1, 3], [2, 3]]不难看出，该结果符合该特征。因此完整代码为

class Solution{
public:
  void dfs(int n, int k, int start){
    if(path.size() == k){
      ans.push_back(path);
      return;
    }
    for(int i = start;i <= n;i ++){
      path.push_back(i);
    dfs(n, k, i + 1);
    path.pop_back();
    }
  }
  vector<vector<int>> combine(int n, int k){
    vector<vector<int>> ans;
    vector<int> path;
    dfs(n, k, 1);  //从1开始选择
    return ans;
  }
};

总结

从上述排列与组合的问题中可以发现，这些问题所使用的回溯算法结构类似，大致结构为

void dfs(所需参数){
  if(路径终止条件){
    将路径结果推入结果容器中;
    return;
  }
  for(int i = 初始（选择）值; 步骤终止条件; i++){
    path.push_back(所处理的对象);
    dfs(所需参数);
    path.pop_back();
  }
}

该结构即经典的回溯算法结构。一般情况下，由于回溯算法与DFS算法及栈结构关系密切，鉴于各个问题的特殊性，该结构中可能会添加visited数组以验证选择情况，或进行剪枝操作等，但该主框架通用于绝大部分可以通过回溯算法处理的问题。