关于完美二叉树的指针填充策略

Question

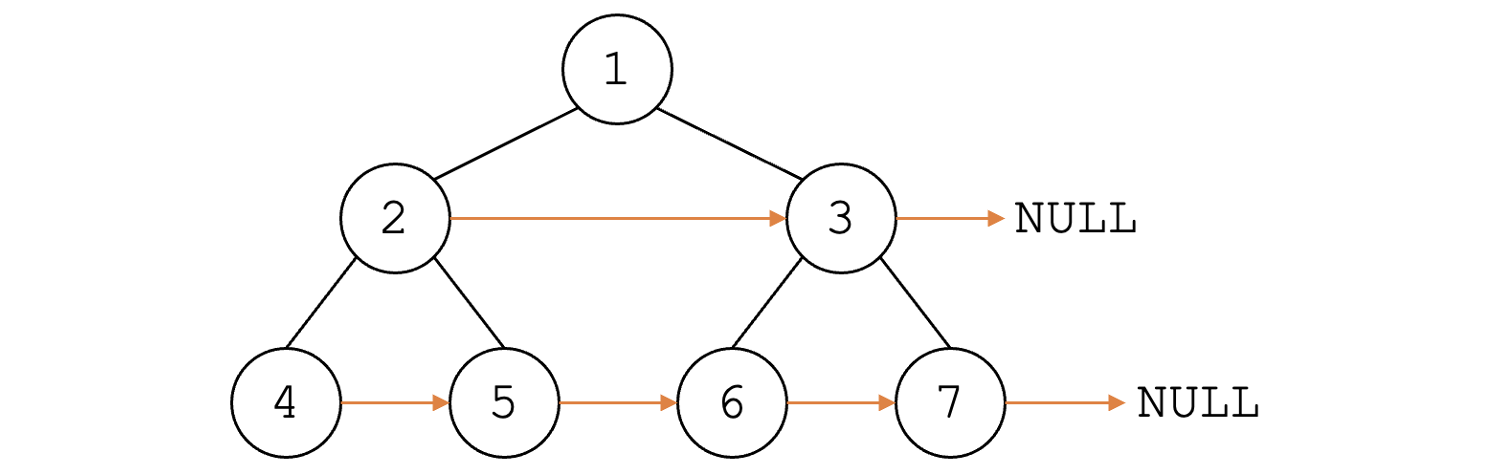
给定一个完美二叉树，其所有叶子结点均在同一层，且每个父节点均有两个子节点，其定义为

struct Node{
  int val;
  Node *left;
  Node *right;
  Node *next;
}

编写算法填充其每个next指针，使该指针指向其下一个右侧节点。若不存在下一个右侧节点，则将next指针设置为NULL。缺省状态下，所有next指针均被设置为NULL。

通过分析完美二叉树的结构，可以发现位于该树每一层最右边的结点的next指针均指向NULL，且均为右节点或根结点。因此

• 若该层最左侧节点为空，则该层不存在
• 若某节点的父节点指向NULL，则该父节点的右节点一定指向NULL

因此，需要通过同时分析两层的状况以进行指针填充操作。即

• 父节点的左节点一定指向其右节点
• 当父节点的next指针不为空时，其右节点指向该父节点的next指针所指向的节点的左节点
• 当父节点的next指针为空时，其右节点也指向NULL

首先，由于指针填充操作需要同时分析两层的状况，因此需要建立反映相邻两层状况的指针cur与pre

Node* cur = root->left->left;
Node* pre = root->left;

当根节点为空时，直接返回空指针，即

if(root == nullptr){
  return nullptr;
}

当根节点不存在子结点时，直接返回根结点。由于该树为完美二叉树，因此若某节点的左节点或右节点不存在，则该节点的子结点均不存在

if(root->left == nullptr){
  return root;
}

对于某节点的左节点，其next指针一定指向该结点的右节点，即

if(root->left != nullptr){
  root->left->next = root->right;
}

对于某节点的右节点

• 若该右节点的父节点的next指针不为空，则该右节点指向其父节点的next指针所指向的节点的左节点，即

if(root->next != nullptr){
  root->right->next = root->next->left;
}

• 若该右节点的父节点的next指针为空，则该右节点的next指针亦为空，即

if(root->next == nullptr){
  root->right->next = nullptr;
}

依据此逻辑，可以通过cur指针与pre指针对根结点的后续节点进行指针填充操作。由于父节点的左节点与右节点均存在，因此cur指针需要沿着next指针向右行进，并对该层其他的父节点执行操作。上文提出，若某层最左侧节点为空，则该层不存在。因此，操作的终止条件为cur指针指向NULL或pre指针指向NULL。

• 当pre指针指向NULL时，所有cur所在层的节点的父节点均遍历完毕。此时，需要将pre指针与cur指针同时推进至下一层，即

pre = cur;
cur = cur->left;

• 当cur指针指向NULL时，cur指针所指节点的左节点不存在，即下一层所有节点均不存在。因此，当前cur指针所在节点为叶子节点，cur指针无法继续前行，整体遍历操作执行完毕

将上述代码段整合后，完整代码为

class Solution{
public:
  Node* connect(Node* root){
    if(root == nullptr) return nullptr;
    else if(root->left == nullptr) return root;
    else{
      root->left->next = root->right;
    }
    Node* cur = root->left->left;
    Node* pre = root->left;
    while(cur != nullptr){
      while(pre != nullptr){
        pre->left->next = pre->right;
        if(pre->next != nullptr){
          pre->right->next = pre->next->left;
        }
        else{
          pre->right->next = nullptr;
        }
        pre = pre->next;
      }
      pre = cur;
      cur = cur->left;
    }
    return root;
  }
};

Python下算法为

class Solution:
  def connect(self, root: 'Node') -> 'Node':
    pre = root
    while pre:
      cur = pre
      while cur and cur.left:
        cur.left.next = cur.right
        if cur.next:
          cur.right.next = cur.next.left
        cur = cur.next
      first = first.left
    return root