通过汉诺塔问题理解递归方法

Question

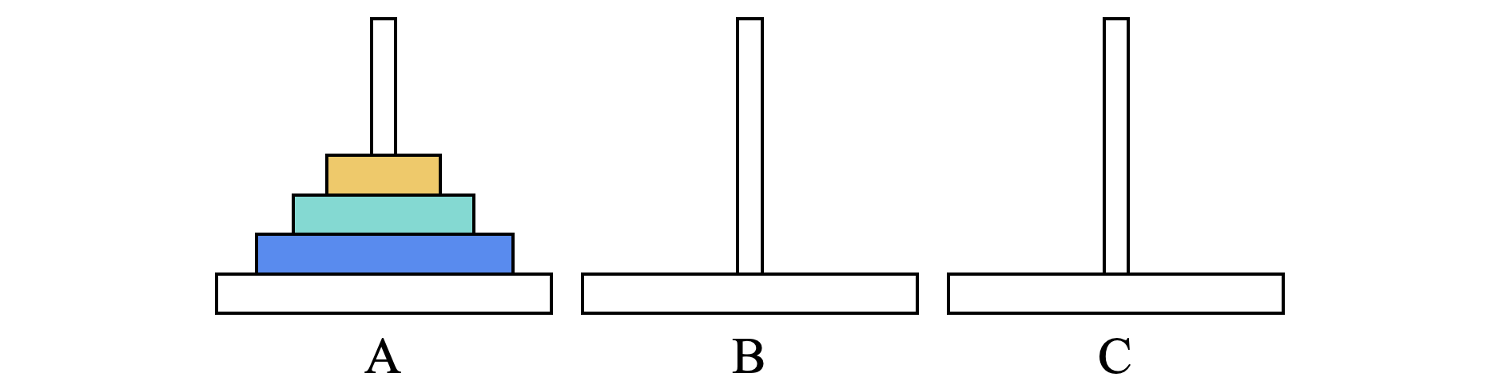
假设存在A、B、C三根杆，汉诺塔问题即需要将位置A上的圆盘全部移动至位置C，在移动过程中每次仅能移动一个圆盘，且三个位置上的圆盘状态始终保持为大盘在下、小盘在上。

假设目标汉诺塔为n阶，当n=3时，其正常流程如下：

• 将小盘移动至位置C，将中盘移动至位置B

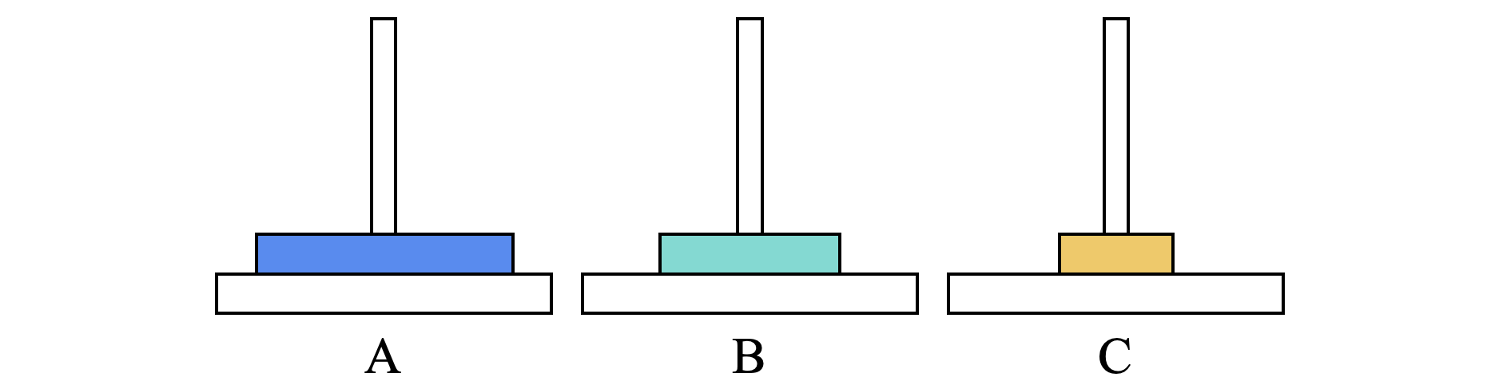
• 将小盘移动至位置B，将大盘移动至位置C

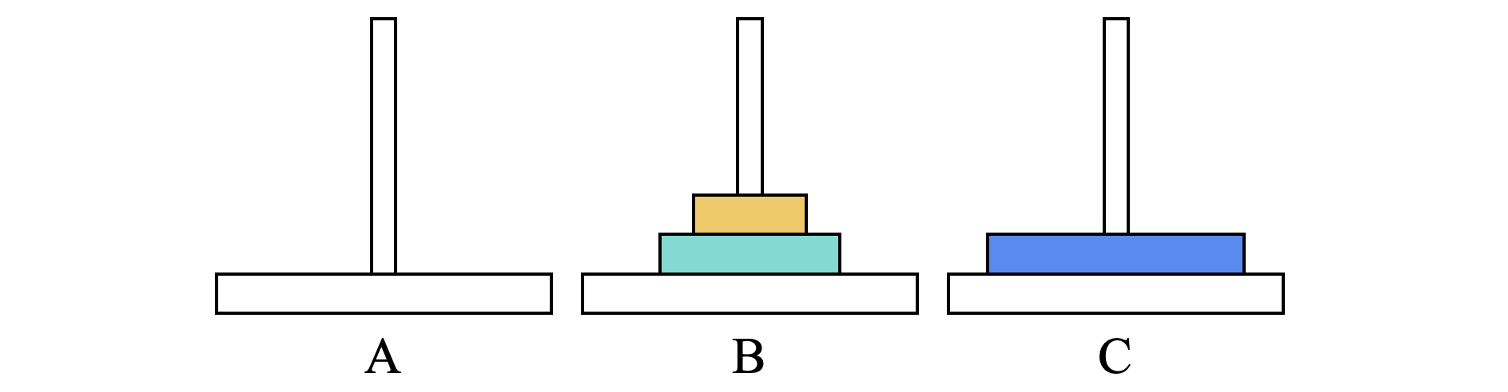
• 将小盘移动至位置A，将中盘移动至位置C

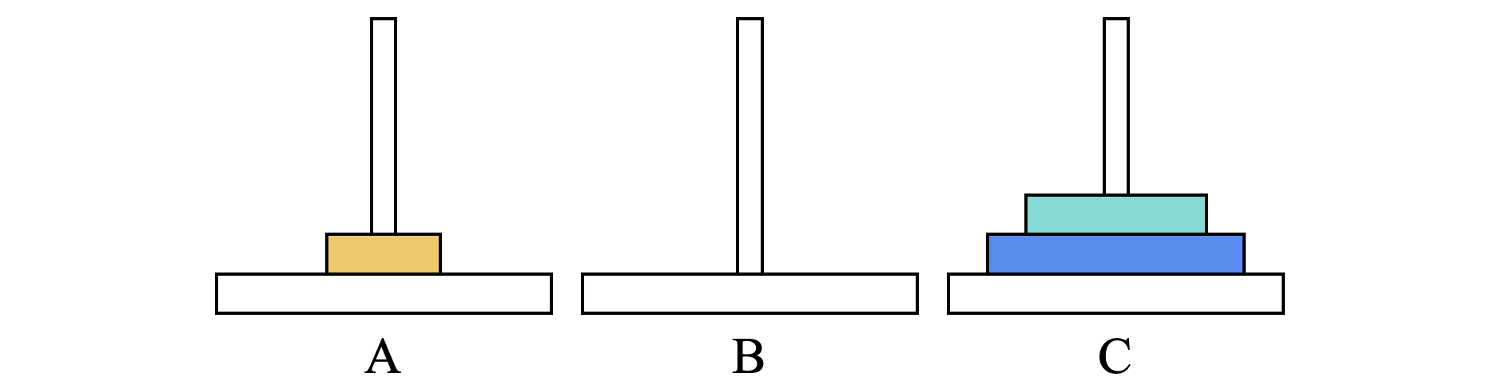
• 将小盘移动至位置C

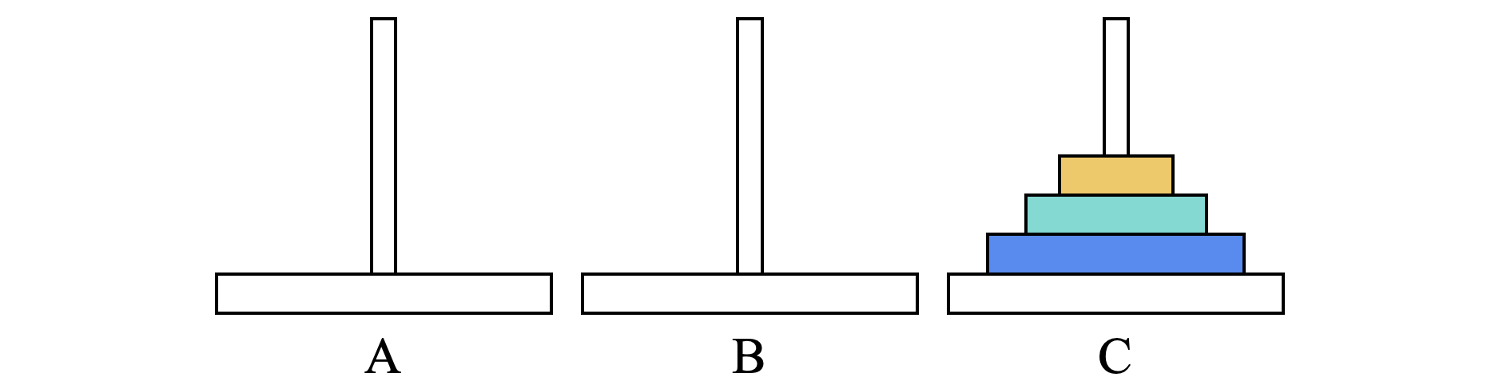
从该过程中可以发现，汉诺塔问题的大致流程为

• 将位置A上除最大圆盘外的n-1个圆盘移动至位置B上
• 将最大圆盘移动至位置C上
• 将位置B上的剩余圆盘移动至位置C上

但由于在移动过程中每次仅能移动一个圆盘，因此步骤一的过程为（步骤三同理）

• 将位置A上第n-1个圆盘上的n-2个圆盘移动至位置C上
• 将第n-1个圆盘移动至位置B上
• 将位置C上的剩余圆盘移动至位置B上

因此，在解决n阶汉诺塔问题前，需要首先解决n-1阶汉诺塔问题。同理，在解决n-1阶汉诺塔问题前，需要首先解决n-2阶汉诺塔问题。如此持续进行会将问题最终转变为一阶汉诺塔问题，即

• 将某位置上的一个圆盘移动至另一个位置上

该操作实际为正常的移动圆盘操作。因此，n阶汉诺塔问题最终被逐渐降阶简化为基础的移动圆盘操作，该过程即计算机算法中的递归操作。

将移动一次圆盘的操作定义为函数move(n, a, b, c),其中n表示该次操作移动的圆盘数量，a表示起始位置，b表示过渡位置，c表示目标位置，则使用递归解决n阶汉诺塔问题的具体流程可用图表示为

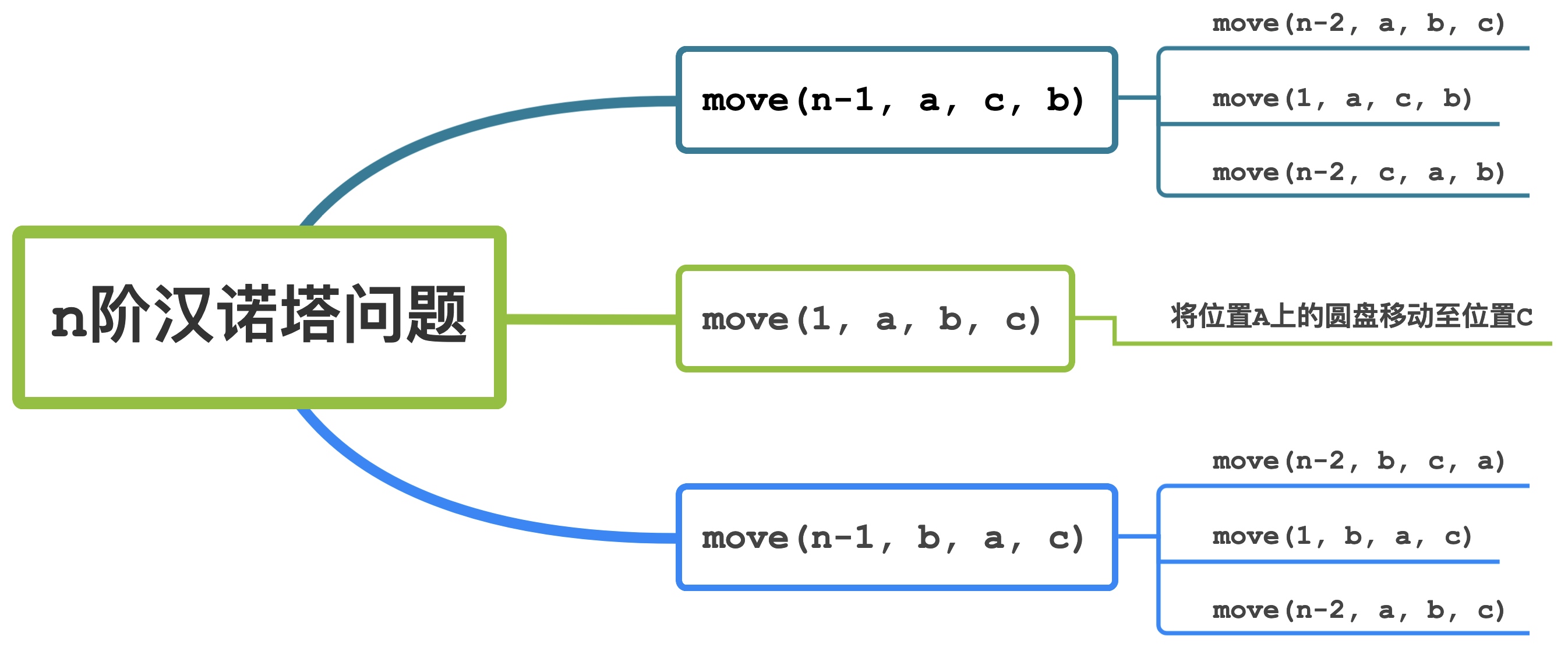
当n=3时，汉诺塔问题的最终流程可用图表示为

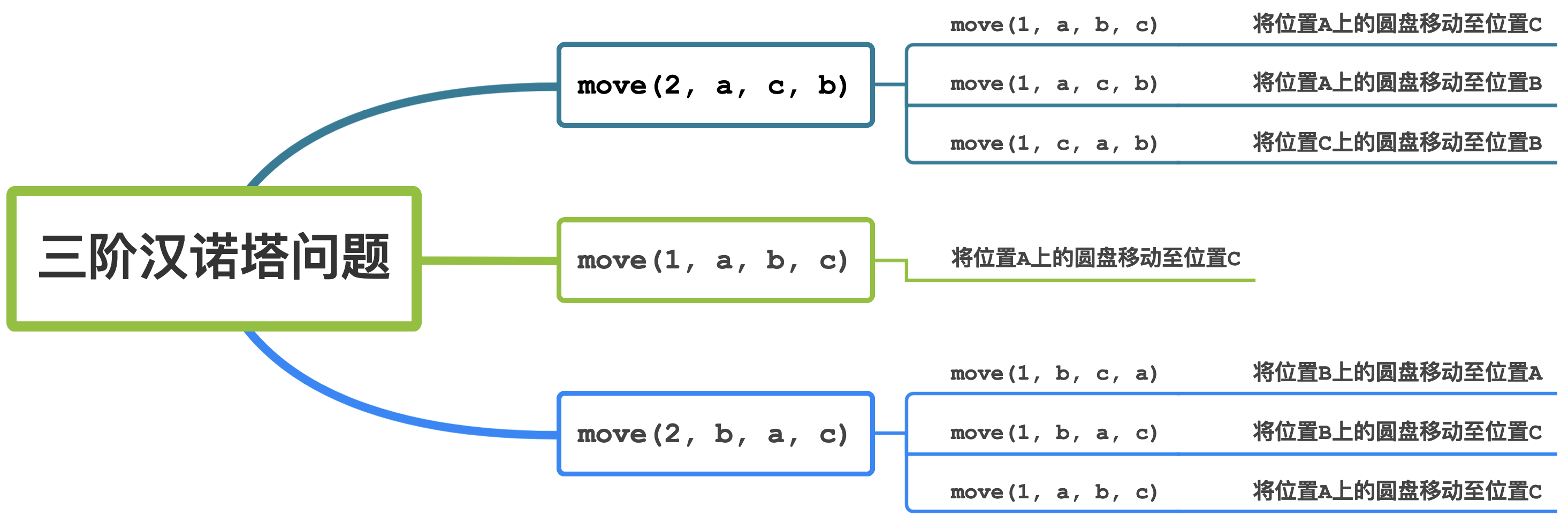
由上述流程可知，每阶汉诺塔问题均能使用同一流程解决。因此，函数move(n, a, b, c)具体内容为

void move(int n, char a, char b, char c){
  if(n == 1){
    printf("%c --> %c", a, c);
  }
  else{
    move(n-1, a, c, b);
    move(1, a, b, c);
    move(n-1, b, a, c);
  }
}

因此，使用递归解决汉诺塔问题的完整代码为

#include <stdio.h>

void move(int n, char a, char b, char c){
  if(n == 1){
    printf("%c --> %c", a, c);
  }
  else{
    move(n - 1, a, c, b);
    move(1, a, b, c);
    move(n - 1, b, a, c);
  }
}

int main(){
  int n = 0;
  scanf("%d", &n);
  move(n, 'A', 'B', 'C');
  return 0;
}

Python下算法代码为

def move(n, a, b, c):
    if n == 1:
        print(a, "-->", c)
    else:
        move(n - 1, a, c, b)
        move(1, a, b, c)
        move(n - 1, b, a, c)


move(int(input()), 'A', 'B', 'C')